Download Word document giving more information on SIZEANAL, as a .ZIP file: 20 kb. Click here.
Download the data sheet as MS-Word file, in zipped form: 3.8 kb
SIZEANAL
Click below to download:
|
Powders are produced or handled in a variety of industries. Particle size distribution (psd) is the single most important property of any powder. This P affects the other two P's of a powder, namely the power consumed to produce the powder and the performance characteristics of the powder. Even if all the particles are spherical, there is always a distribution of sizes present. To complicate matters, all industrial powders are non-spherical in shape. Have you ever wondered, what is the particle size of the paper-weight present on your table; or, what is the particle size distribution of dust inhaled by you and what portion of this distribution enters your lungs? If you do not have the answers to these simple questions, just imagine how complex would powders be that contain particles of a wide distribution of shapes and sizes. Knowing the particle size distribution is of vital importance to industries like cement, minerals, ceramics, coal and ash (thermal power), fertilizer, polymers, toners, catalysts, dyes and pigments, cosmetics, pharmaceuticals, pesticides, detergents, chemicals, refineries, dairy products, beverages etc., manufacturers of equipments like grinding mills, classifiers, cyclones, bag filters, ESP's, boilers, kilns and reactors, spray dryers, powder mixers, pollution control equipments etc., and test houses, R&D labs, consultants, designers etc. Several expensive instruments are available to measure the psd of a powder like Coulter counter, Photosedimentometer, X-ray Sedigraph, Laser-based instruments, Microscopy etc. Even if you do posses any of these instruments, do you know that you can use one instrument's data to predict the information given by all the other instruments, and more? Each instrument measures one particular psd of a powder (from among a variety of different psd's possible!) and therefore the measurements of one instrument do not tally with those of another. We have identified all these problems and done fundamental research establishing correlations among different instruments and further, to predict some powder properties not measured by any of these instruments. All these features are incorporated into the software SIZEANAL. These have also received international recognition by way of research papers published, and fetched Outstanding Consultant Award of Rs 20,000 in the year 1989. The following powder parameters are predicted by SIZEANAL :
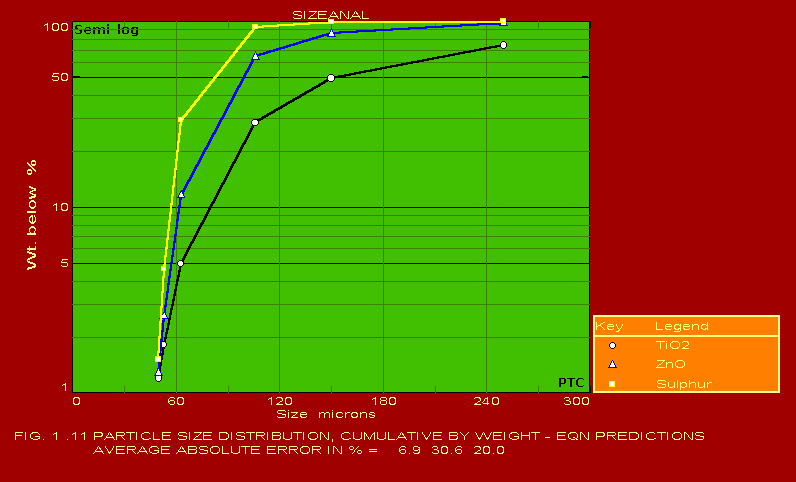
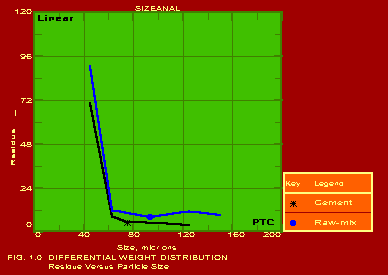
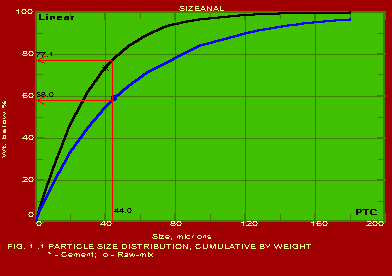
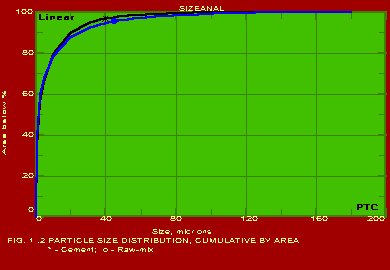
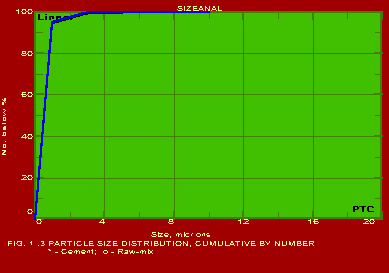
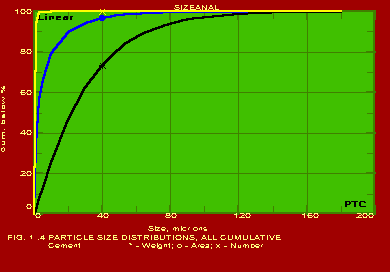
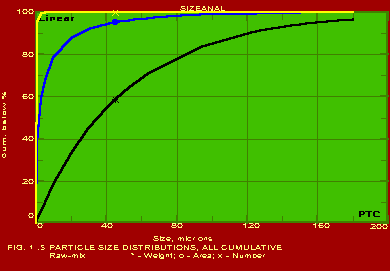
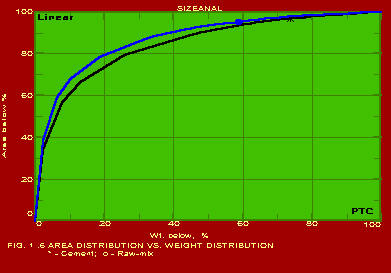
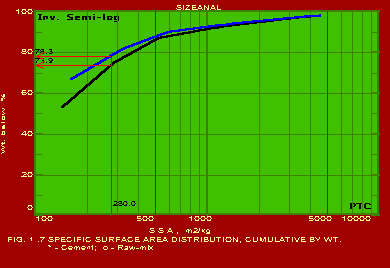
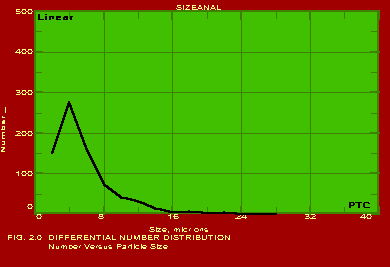
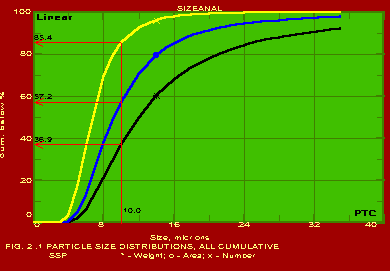
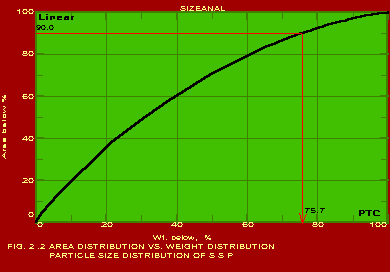
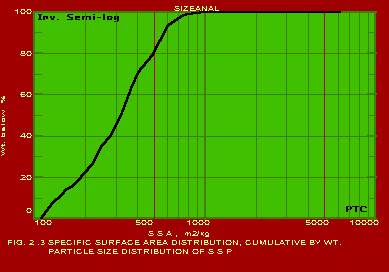
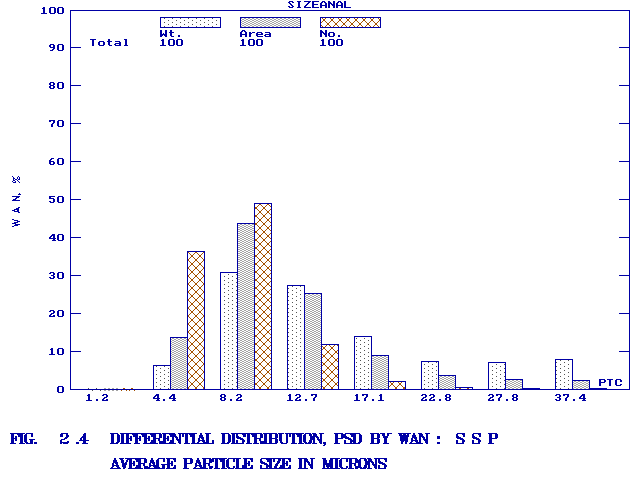
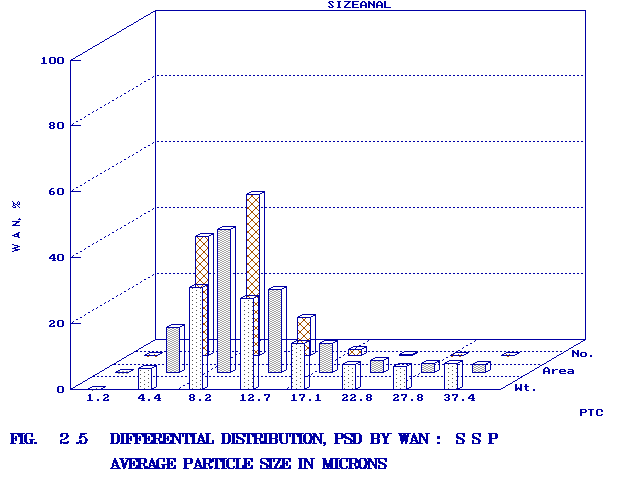
The various methods and calculational procedures employed in SIZEANAL are presented in our technical report No. PTC:02-1. The effect of particle shape is also accounted for in SIZEANAL. The fact that finer particles are more spherical than coarser ones is also considered. This can have important ramifications where one instrument is used for measurements (like a Coulter counter which measures the volume diameter of particles) whereas the application area may require a different particle diameter (like cyclone operation where the important diameter would be the Stokes diameter). The measurements of Coulter counter in such a case would be directly useful only if all the particles are exactly spherical. For any practical powder containing non-spherical particles, the use of SIZEANAL would be necessary to first convert the measured volume diameters into their corresponding Stokes diameters before applying the results for cyclone design and optimisation. We are competent to identify the particle diameter and distribution measured by your instrument as well as the same required for your specific application on hand, and use SIZEANAL appropriately. We have used SIZEANAL to give consultancy and advice to hundreds of industries to solve their powder-related problems, optimise grinding mills, spray dryers, cyclones/hydrocyclones/classifiers etc. The software can be used with the raw data of any one instrument to obtain the results of all the other instruments. Typical graphical outputs of SIZEANAL are shown below for the "raw data" of two instruments, namely Sieving set and Microscope. Two powders (cement and raw-mix) were measured with a sieving set and the raw measurements of residues on individual sieves versus the particle size (sieve aperture size) are shown in Fig. 1.0. These "raw data" are used to obtain the complete particle size distribution (psd) information, and these are shown in Figs. 1.1- 1.7 below. Another powder (Single Super Phosphate) was measured using a microscope and the number of particles in individual particle size ranges (Martin's diameter) are shown in Fig. 2.0. These "raw data" are again used to obtain the complete psd information as shown in Figs. 2.1- 2.3. It may be noted from the graphs that the software can be used to instantaneously show any set of data in Linear, Log-log, Semi-log and Inverse Semi-log scales. Further, it may be seen from Figs. 1.1 and 2.1 that SIZEANAL permits calculation of y-value for any specified x-value as well as back-calculation of x-value for any desired y-value. This is especially useful to instantly estimate the median values (d50) of the psd's. The differential distributions by WAN for
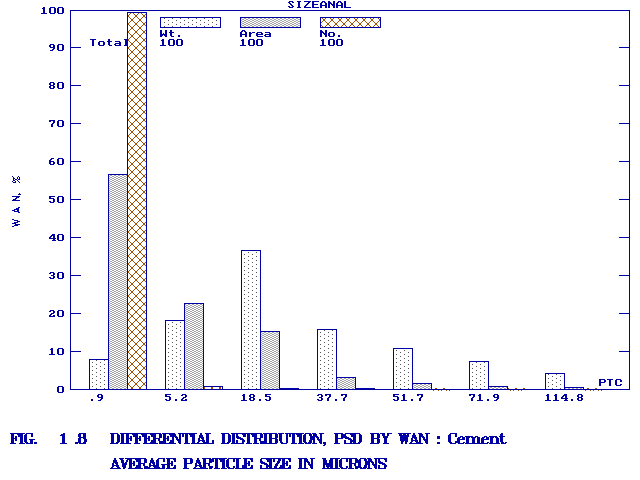
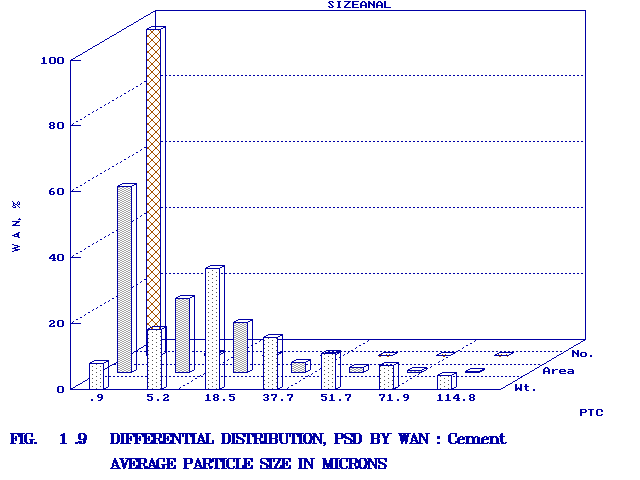
cement and SSP are shown in Figs. 1.8-1.10 and Figs. 2.4-2.6
in three different formats respectively. For cement, Rosin-Rammler
equation with an exponent close to 1, and for SSP, the monotonic
equation with an exponent close to 2 are obtained. From the bar
graphs shown in Figs. 1.8 and 1.9, it can be seen that
for cement, while the number distribution is all concentrated
practically in the finest size interval, the area distribution falls
exponentially, the weight distribution follows the well-known
"bell-shaped" curve. However, for SSP in Figs. 2.4
and 2.5, all three of the WAN-curves are "bell-shaped"
with the steepness being the greatest for number and lowest (or most
gradual) for weight distribution. These conclusions are specific
only to the two powders analysed here and should by no means be treated
as generally applicable to all cement and SSP powders. The
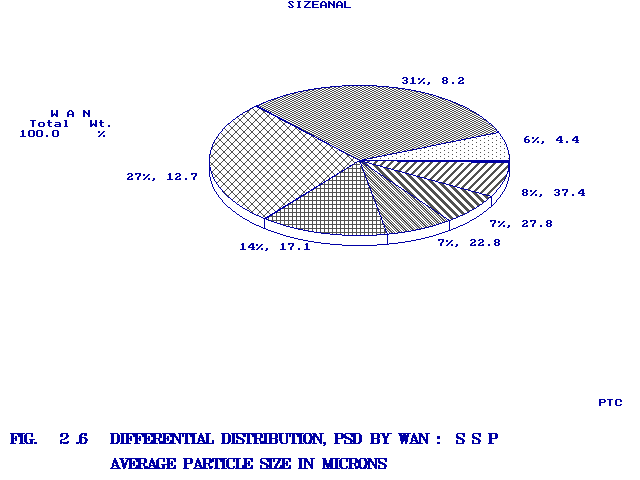
representation of psd in the form of pie-graphs as shown in Figs. 1.10
and 2.6
is also unique and is an integrated feature in SIZEANAL.
The various graphs amply demonstrate the power of SIZEANAL and
without them, the knowledge of your powders is certainly incomplete. |
 |
|||||||||||||||||||||||||||||||||||||||||||
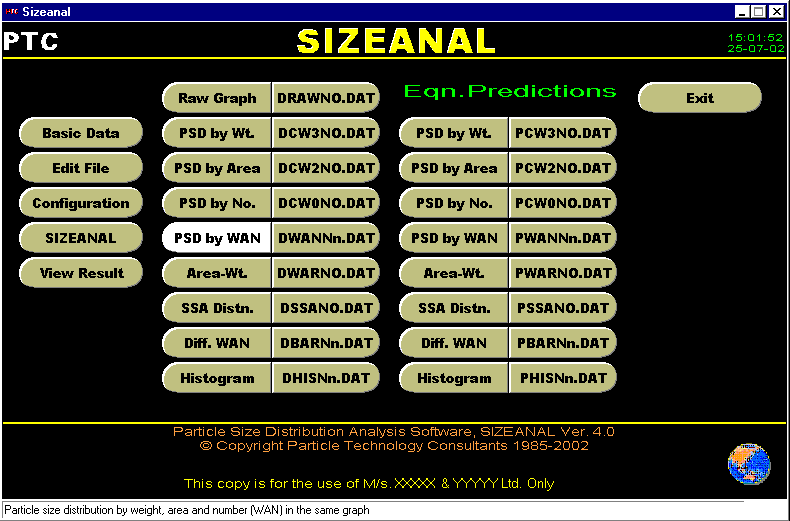
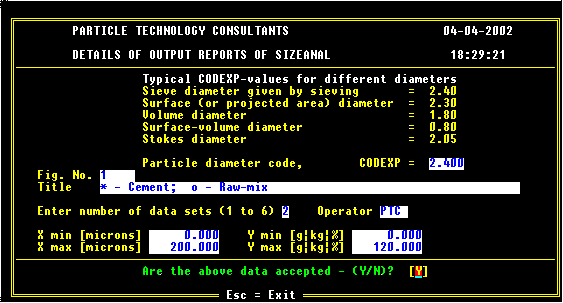
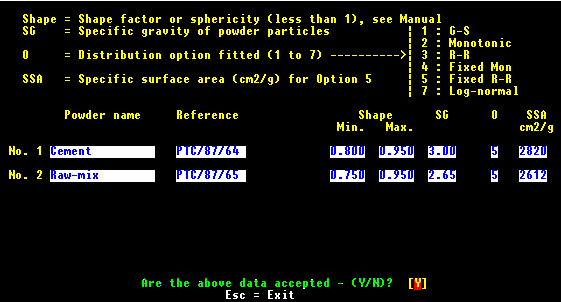
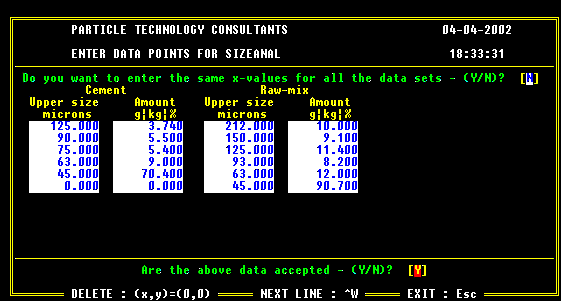
The following show the various data that are to be entered during Data Entry.
 |
 |
 |
The following is a screenshot of SIZEANAL's graphics screenshot. |
 |
 |
The following graphs are obtained using the various menu options shown in the SIZEANAL's Opening Menu shown above.
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |