Home

1. CURVE-FIT:   Based on a novel monotonic transform
2. LINEFIT     :   Based on linear regression
3. QUADFIT   :   Based on quadratic regression
4. LOGFIT     :   Based on logarithmic regression
5. EXPOFIT   :   Based on exponential regression
6. RRMFIT     :   Based on Rosin-Rammler regression
7. POLYFIT    :  Based on polynomial regression
8. POSYFIT    :  Based on posynomial regression
9. RECIFIT      :  Based on reciprocal-posynomial regression
10. MULTFIT     :  Based on multi-variable linear and logarithmic regression

The software module CURVEFIT in GITA is based on a novel mathematical technique of monotonic transform developed and published in international research journals.  It is essentially useful for determining mathematical correlations between data, interpolation and extrapolation, forecasting, developing simple analytical equations for complex integrals (which can otherwise be calculated only using advanced numerical techniques), developing simple equations for infinite series solutions (which are encountered in several engineering problems), parametric studies etc.  The software has excellent graphing capabilities with possible instant representation in different forms like Linear, Log-log, Semi-log and Inverse Semi-log scales.  It also has in-built features for storage and management of data.

The following are some of the areas where GITA has been successfully applied:

• Particle size distribution of powders

• Classifier efficiency curves

• Cement strength development curves

• Ball mill grinding rates

• Ball mill chamber sampling

• Kiln operation curves

• Coal calorific value estimation

• Valve calibration curves

• Product yield curves in petroleum isocracking process

• Ammonia density versus pressure and temperature

• Drying rate curves and diffusivity estimation

• More accurate relation than Arrhenius relation for reaction rate constant versus temperature

• Langlier index estimation for cooling water quality and scaling

• Semi-variogram curves

• Release rates of drugs

• Correlations for psychrometric relations

• Filter life estimation

• Compression ratio of working fluid in heat pumps

• Correlations for predicting the amount in the desired particle size range in the final product and its moisture content versus several operating variables

• Sale forecasting for FMCG, pharmaceutical companies etc.

• Simpler relation for Normal probability integral and other integrals

• Simpler relation for several infinite series solutions encountered in engineering

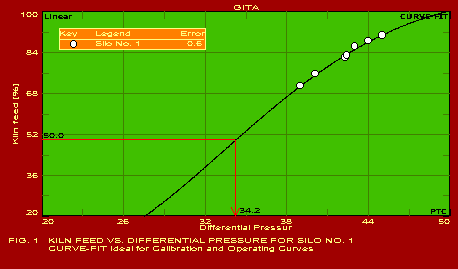
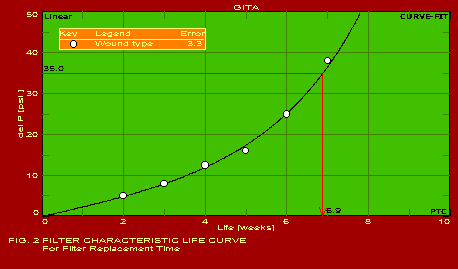
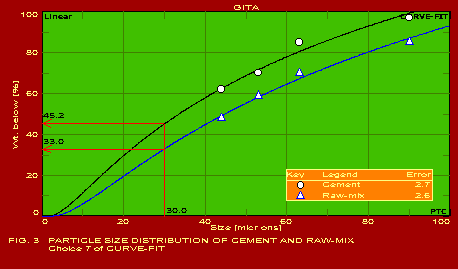
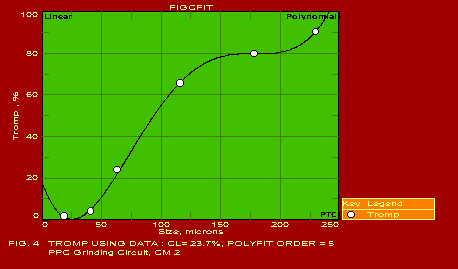
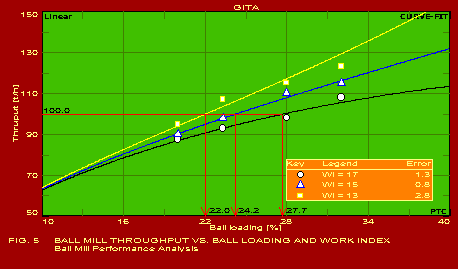
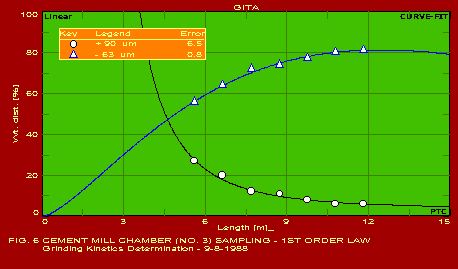
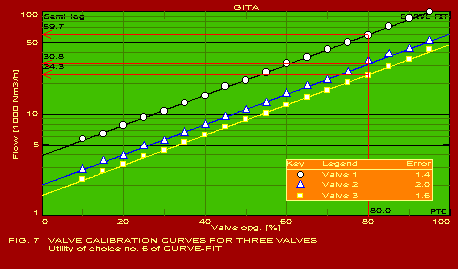
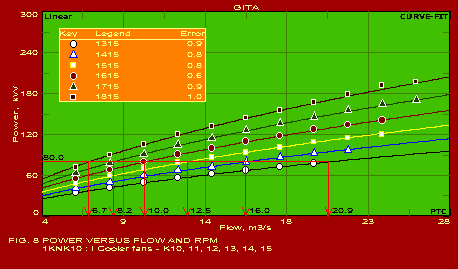
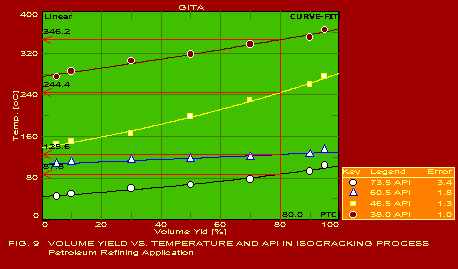
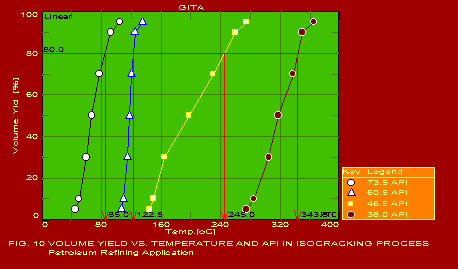
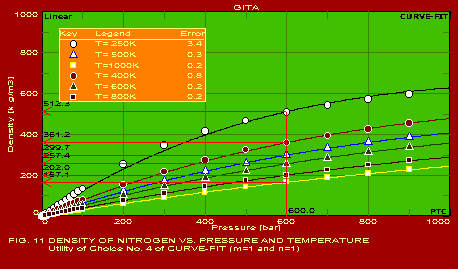
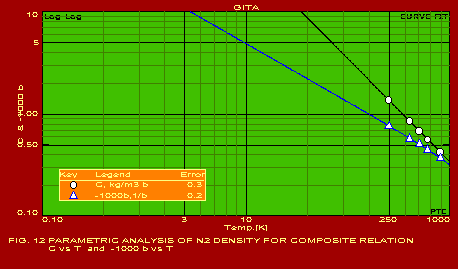
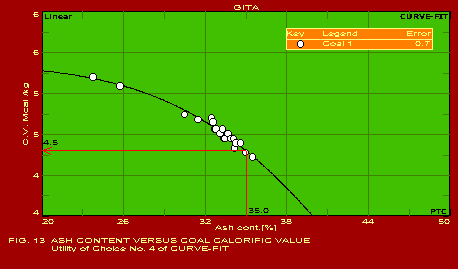
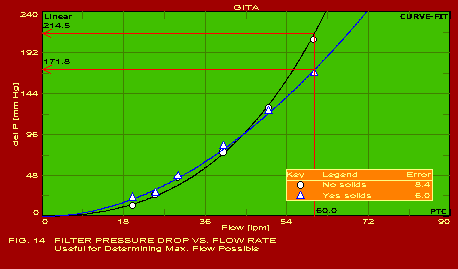
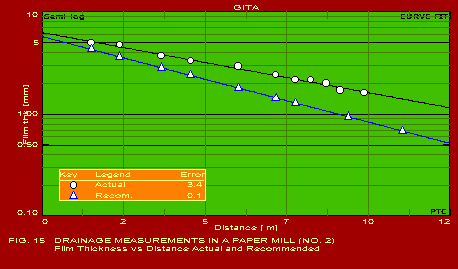
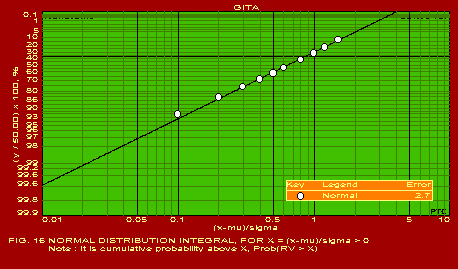
A summary of the actual values of the parameters estimated for typical applications, which should be found useful by users in the respective industries, is given below.  The following summary refers to the predictions obtained with only one of the pack of seven packages included in GITA, namely CURVEFIT.  The other packages are also useful for specific applications.  It may be noted that the error in the predictions is extremely reasonable in all the cases which is indicative of the power of this software.  The actual graphs showing the predicted curves along with the data points are also shown for 13 of the 16 applications mentioned below. 

The package includes a module called FASTFIT, which enables quick determination of the best package from among the various packages listed earlier.  This leads one to the package most suitable for a particular application.  After running FASTFIT, one can refine the mathematical equation by going into the best package suitable for the application.  

GITA also incorporates an automatic inverse determination feature, wherein mathematical equations can be obtained for predicting the x-value for a given y-value, in other words, x = f ^-1(y) is determined.

The MULTFIT module in GITA is useful for determining a mathematical equation between several independent variables and one dependent variable:

       y = f (x₁,x₂,x₃,x₄,...)

The functional form can be either linear or logarithmic as follows:

       y = a₀ + a₁x₁+ a₂x₂+ a₃x₃+ a₄x₄+ ...

       y = C  x₁^a1 x₂^a2 x₃^a3 x₄^a4...

The latter form mentioned above is especially useful in dimensional analysis to establish dimensionless correlations in process studies.  Running MULTFIT gives both the above correlations along with the corresponding average absolute error values.